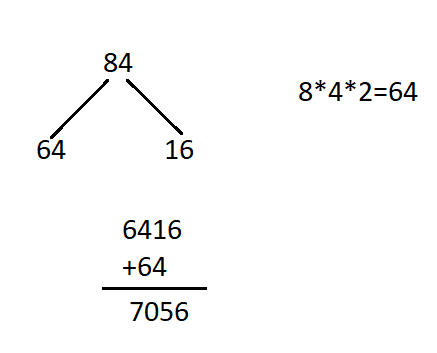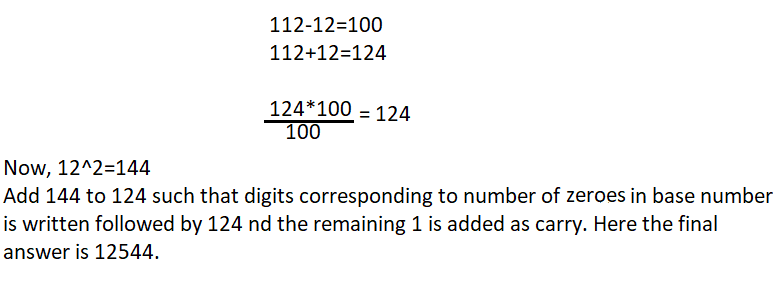Short Tricks to Find Squares and Square Root in Bank Exam

Shortcut tricks for squares, square roots, and multiplication are very important for any competitive exam. Candidates aspiring to appear for competitive bank exams like IBPS PO, SBI PO, etc. will require these shortcut tricks in the Quantitative Aptitude section. Simplification must be done faster to save time, and hence these shortcut methods will help you score better for bank exams or any upcoming Government exams. In this article, we will learn some Short Tricks to Find Squares and Square Root for Bank Exam 2020. Check them out and learn with us!

How to find the square of a number? Shortcut method  

Here we will learn to find the square of any number less than 1000, which is more than enough for any upcoming competitive exams. Let’s group the numbers into two categories –

1. Less than 100 – For any number less than 100 follow the following steps: 

• Split the number and find the square of each digit separately.
• Now write these numbers together. Write both ones and tens place of each number(say, if it’s 32, write as 09).
• Now find the double of the product of each digit in the base number
• Add this to the answer obtained in step 2 after leaving one’s place at the right.
• The sum will give you the final answer.

Check out these examples for better understanding:

Example 1: Find the square of 84.

Hence, the square of 84 is 7056

2. Greater than 100 – Follow the steps given below:

• Check for the nearest number having zeroes, for example, take 112. Here the nearest number to this having zero is 100. 
• So get two numbers from the base number by adding and subtracting 12, the numbers here would be 100 and 124.
• Remember the square of the number added or minimized in the last step, here 122=144
• Go back to step 2 and multiply 100*124 and divide the product to remove the zeroes. Here there are two zeroes and hence divide with 100. 
• Now 124*1=124, and now just write 44 after 124 and add 1(of 144) to the next digit left, ie final answer is 12544. Here as we divided with 100( having two zeroes) we appended two digits of 144, and the remaining as carry.  

Here consider the base number as 100, as it is closest to 112.

Check here why most candidates fail to qualify IBPS bank exams 

How to find the square root of a 4-digit number? – Shortcut method

First, we need to remember the unit digits of all squares from 1 to 10. The figure below shows the unit digit of squares:

 Let’s learn this shortcut method with a few examples: 

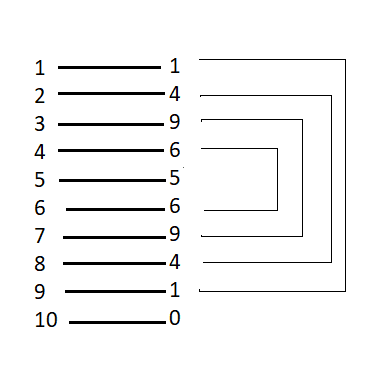
Example 1: Find the square root of 4624.

Follow the following procedure step by step

• We initially group the last pair of digits, and then the remaining digits together.
• Check of its unit digit place ie 4, hence the square root ends in 2 or 8.
• Consider the first two digits – 46. It lies between 6^2 and 7^2 ( 36<46<49)
• Hence the ten’s digit of the square root will be 6. 
• Now, we need to find whether it is 62 or 68. For that multiply 6 and its next term in series ie 7. 

                                                             6*7=42<46

• Since 46 is bigger than 42, the square root of 4624 will be bigger of the two options ie 68.

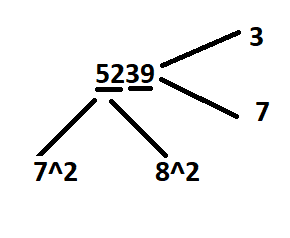
Example 2: Find the square root of 5329.

• We initially group the last pair of digits, and then the remaining digits together.
• Check for its unit digit place ie 9, hence the square root ends in 3 or 7.
• Consider the first two digits – 53. It lies between 72 and 82 ( 49<53<64)
• Hence the ten’s digit of the square root will be 7. 
• Now, we need to find whether it is 73 or 77. For that multiply 7 and its next term in series ie 8. 

                                                             7*8=56>53

• Since 53 is smaller than 46, the square root of 5329 will be smaller of the two options ie 73.

How to find the square root of 5-digit numbers? – Shortcut method

Let’s learn by solving two examples

Example 1: Find the square root of 19321.

• We initially group the last pair of digits, and then the remaining digits together.
• Check of its unit digit place ie 1, hence the square root ends in 1 or 9.
• Consider the first three digits – 193. It lies between 13^2 and 14^2 ( 169<193<196)
• Hence the first two digits of the square root will be 13. 
• Now, we need to find whether it is 131 or 139. For that multiply 13 and its next term in series ie 14. 

                                                             13*14=142<193

• Since 193  is bigger than 142, the square root of 19321 will be bigger of the two options ie 139.

Example 2: Find the square root of 14161.

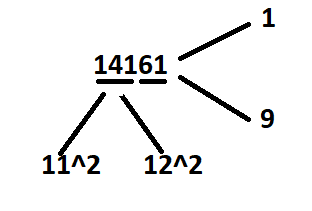
• We initially group the last pair of digits, and then the remaining digits together.
• Check of its unit digit place ie 1, hence the square root ends in 1 or 9.
• Consider the first three digits – 141. It lies between 11^2 and 12^2.
• Hence the first two digits of the square root will be 11. 
• Now, we need to find whether it is 111 or 119. For that multiply 11 and its next term in series ie 12. 

                                                             11*12=132<141

• Since 141 is bigger than 132, the square root of 19321 will be bigger of the two options ie 119.

Entri app recently launched a comprehensive study package for all the upcoming bank exams in 2020-21- BANKING 2.0. Enroll in the course and pass your exam with flying colors. Download the app for all the important notifications regarding Bank/Government Exams.