Table of Contents
In this article, we will discuss the Basics of Vectors which is one of the very important topics that need to be covered in the preparation for competitive exams. Here we shall cover the basics and definition of vectors. We will also have a look at the meaning of a vector by understanding the basic components of a vector.
Prepare for various Government exams! Download Entri App!
Basics of vectors Notes
While studying math and physics, we come across two types of quantities namely scalars and vectors. The quantity that consists of only value or magnitude but no direction is a Scalar quantity, for example, length, mass, speed, area, etc. On the other hand, the quantity that involves magnitude, as well as direction, is a Vector quantity, for example, displacement, velocity, acceleration, force, weight, momentum, etc.
Basic Definition a Vector
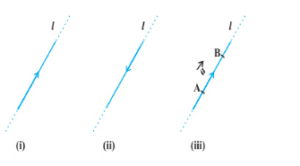
Fig. 1
- A measure that has magnitude, as well as direction, is called a vector. From the figure above, the directed line segment shown in Figure 1 (iii) is a vector.
- It is represented as ‘vector AB→’ or ‘vector a→ ’.
- point A from where the vector AB→ begins is called its starting or initial point, and point B where it terminates is called its end or terminal point.
- The distance between these two points of a vector namely the initial and terminal is called the magnitude or length of the vector, denoted as |a→ |, or |AB→| or The arrow indicates the vector’s direction.
Note: Length is always positive or never negative. Hence, AB→ | is always ≥ 0.
Meaning of Position Vector
Have a look at the following diagram below
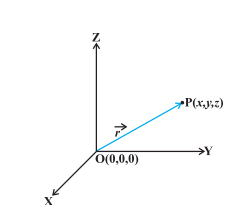
Fig.2
- Figure 2 shows a right-handed rectangular or Cartesian coordinate system.
- Let’s consider a point ‘P’ in space, such that its coordinates are (x, y, z) with respect to the origin O (0, 0, 0).
- The position vector of the p with respect to the O is the vector OP→, where O is the starting point and P is the end point of the vector.
- As we already know about the distance formula. We will apply it to find the magnitude of OP→ or r→ , here, we get
|OP→| = x2+y2+z2−−−−−−−−−−√
In practice, the position vectors of points A, B, C, … with respect to the origin O are denoted by a→ , b→ , c→ , …. as shown below.
Prepare for various Government exams! Download Entri App!
Direction Cosines
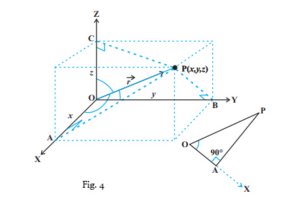
Next, have a look at the figure below
- Figure 4 shows a position vector OP→ (or r→ ) of a point P (x, y, z). The vector r→ makes angles α, β, and γ with the positive directions of the x, y, and z-axes respectively. These are called direction angles. Now, the direction cosines of the vector r→ are the cosine values of these angles. They are denoted as:
- l = cosα
- m = cosβ
- n = cosγ
- Another thing that you may note from the same, is that the triangle OAP is a right-angled triangle. Hence, we have
- cosα = xr, where r stands for |r→ |.
- Similarly, from the right-angled triangles OCP and OBP, we have cosβ = yr and cosγ = zr
Therefore, the coordinates of the point P can be given as (lr, mr, nr). These numbers, lr, mr and nr, are proportional to the direction cosines of the vector r→ . They are called direction ratios of the r→ and are represented as a, b, and c respectively.
Entri app provides you with best practice questions for the complete preparation of various competitive exams. For the complete preparation, download the Entri app and start preparing.
Our R&D team provides the best material and books for the complete preparation of all government exams. We provide PDFs of the previous year’s question papers with solutions and detailed analysis. All you need to do is download the Entri app and start practicing.