HCF and LCM is one of the most frequently asked topics in most of the exams. HCF stands for Highest Common Factor. It is the greatest number that divides each of the two or more numbers. HCF is also called the Greatest Common Measure (GCM) and Greatest Common Divisor (GCD). LCM stands for Least Common Multiple. It is the smallest common multiple of any two or more numbers. Here are more details on them and some of the LCM and HCF questions for Bank exam 2020.
HCF of numbers can be found out using two methods:
- Prime factorization method
- Division method
HCF by Prime factorization Method:
Step 1: Write each number as the product of its prime factors (Hence the name prime factorization method)
2: List the common factors of each number.
3: The product of all the common prime factors in the smallest power is the HCF.
For example,
Find the HCF of 42,63 and 140. (L.I.C.A.D.O 2008)
42 = 2x3x7
63 = 3x3x7
140 = 2x2x5x7
Therefore, the common factor with the least power is 7. Hence, HCF is 7.
HCF by Division Method:
Step 1: Divide the larger number by smaller one.
2: Divide the divisor by the remainder.
3: Repeat the process of dividing the preceding number by the remainder last obtained till zero is obtained as the remainder.
Finding HCF of three or more numbers:
Suppose we have to find the HCF of three numbers.
Step 1: Find the HCF of any two numbers.
2: Now, repeat the process with this new HCF and the third number to get the HCF of all the three numbers.
For example,
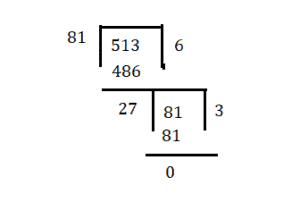
Find the HCF of 513,1134,1215.
Step 1: HCF of 1134 and 1215
2: Required HCF = HCF of (HCF of 1134,1215) and 513.
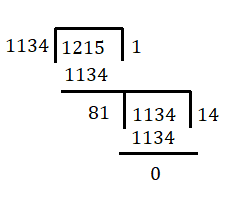
Hence, required HCF is 27.
LCM can be found using two methods:
- Factorization method
- Common division method (short cut method)
LCM by Factorization Method
Step 1: Resolve each one of the given numbers into products of prime factors.
2: LCM is the highest powers of all the factors.
For example,
Find the LCM of 87 and 145.
87 = 3×29
145 = 5×29
Therefore, LCM = 3x5x29
= 435.
LCM by Common Division Method
Step 1: Arrange the given numbers in a row in any order.
2: Divide by a number which divides exactly at least two of the given numbers and carry forward the numbers which are not divisible.
3: Repeat the above process till no two of the numbers are divisible by the same except 1.
4: The product of the divisors and the undivided numbers is the LCM.
For example,
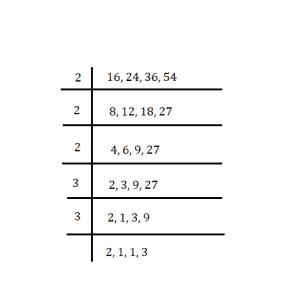
Find the LCM of 16,24,36 and 54.
Hence, LCM = 2x2x2x3x3x2x1x1x3 = 432.
Some of the important points to keep in mind:
Product of two numbers = Product of their HCF and LCM
HCF of fractions = HCF of numerators/ LCM of denominators
LCM of fractions = LCM of numerators / HCF of denominators
Prepare for all exams using Entri app
LCM and HCF Questions for Bank Exam 2020
Here are some questions that appeared in various examinations:
1.Find the LCM of 2x2x3x3x3x5x7x7, 2x2x2x3x3x5x5x7x7x7x7, 2x3x5x5x5x7x11 (L.I.C.A.D.O ,2008)
Answer: LCM = Product of highest powers of 2,3,5,7 and 11
= 2 x 2 x 2 x 3 x 3 x 3 x 5 x 5 x 5 x 7 x 7 x 7 x 7 x 11
2.Two numbers are in the ratio 3:4. Their LCM is 84, Find the numbers (SSC, 2010)
Answer: Let the numbers be 3x and 4x. Then, their LCM = 12x
So, 12x = 84 or x=7
Therefore, the numbers are 21 and 28.
3. The HCF of two numbers is 11 and their LCM is 693. If one of the numbers is 77, find the other. (PSC,2009)
Answer: Product of numbers = Product of their HCF and LCM
77x = 11*693
X = (11*693)/77 = 99.
4. Find the least number which is exactly divisible by 32,36,45,60 and 80 (RRB 2006)
Answer: Required number = LCM of 32,36,45,60,80
= 2x2x2x3x5x3x2x2
= 1440.
5.Find the smallest number which when increased by 10 is completely divisible by 12, 15, 18, 20 and 24. (PCS 2006)
Answer: Required number = LCM of (12, 15, 18, 20, 24)-10
= 360-10
= 350.
Check this article to learn more about how to improve calculation speed to crack the bank exams
6. Find the greatest number of five digits which is divisible by 15, 21 and 36. (PCS 2006)
Answer: Greatest number of five digits = 99999
Required number must be divisible by LCM of 15, 21, 36 = 1260
On dividing 99999 by 1260, we get 459 as remainder.
Required number = 99999-459 = 99540.
7. Find the largest number of five digits which when divided by 16, 24, 30 or 36, leaves the same remainder 10 in each case. (CPO 2007)
Answer: Largest five-digit number = 99999
LCM of 16, 24, 30, 36 = 720
On dividing 99999 by 720, remainder obtained = 639
Thus, largest number of five-digits divisible by 16, 24, 30, 36 = 99999-639 = 99360
Hence, required number = 99360 + 10 = 99370.
8. Seema, Meena and Reema begin to jog around a circular stadium and they complete their revolutions in 54 seconds, 42 seconds and 63 seconds respectively. After how much time will they come together at the starting point? (Bank P.O 2010)
Answer: LCM of 54, 42 and 63 = 378
So, the three girls will come together at the starting point in 378 seconds i.e., 6 minutes 18 seconds.
9. The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they all change simultaneously at 8:20:00 hours, then at what time will they again change simultaneously? (RRB 2006)
Answer: Interval of change = LCM of 48,72,108 = 432 seconds.
So, the lights will again change simultaneously after every 432 seconds, i.e., 7 minute 12 seconds. Hence, next simultaneous change will take place at 8:27:12 hours.
10.When Seeta made necklaces of either 16 beads, 20 beads or 36 beads, not a single bead was left over. What could be the least number of beads Seeta had? (Bank recruitment 2008)
Answer: Required number of beads = LCM of 16, 20, 36 = 720.