Table of Contents
In Python, it is very easy to implement stack and queue data structures. Stack is called LIFO because Stack works on the principle of “Last-in, first-out” and Queue is called FIFO because Queue works on the principle of “First-in, first-out”, and the inbuilt functions in Python make the code shorter and simple.
The Queue module implements multi-producer, multi-consumer queues and it is especially useful in threaded programming when information must be exchanged safely between multiple threads. The Queue class in this module implements all the required locking semantics and it depends on the availability of thread support in Python.
This module implements three types of queue, which differ only in the order in which the entries are retrieved. For FIFO queue, the first tasks added are the first retrieved and for LIFO queue, the most recently added entry is the first retrieved (operating like a stack). And for priority queue, the entries are kept sorted and the lowest valued entry is retrieved first.
Learn Coding in your Language! Enroll Here!
This queue module defines the following classes and exceptions.
class Queue.Queue(maxsize=0)
This is a constructor for a FIFO queue. Argument maxsize is an integer that sets the upper bound limit on the number of items that can be placed in the queue. Insertion will block once this size has been reached, until queue items are consumed. If maxsize is less than or equal to zero then the queue size will be infinite.
class Queue.LifoQueue(maxsize=0)
This is constructor for a LIFO queue. Argument maxsize is an integer that sets the upperbound limit on the number of items that can be placed in the queue. Insertion will block once this size has been reached, until queue items are consumed. If maxsize is less than or equal to zero then the queue size will be infinite.
class Queue.PriorityQueue(maxsize=0)
This is constructor for a priority queue. Argument maxsize is an integer that sets the upperbound limit on the number of items that can be placed in the queue. Insertion will block once this size has been reached, until queue items are consumed. If maxsize is less than or equal to zero then the queue size is infinite.
exception Queue.Empty
This line indicate that the exception raised when non-blocking get() (or get_nowait()) is called on a Queue object which is empty.
exception Queue.Full
This line indicate that the exception raised when non-blocking put() (or put_nowait()) is called on a Queue object which is full.
Queue Objects
Queue.qsize()
This function returns the approximate size of the queue.
Queue.empty()
This function returns True if the queue is empty otherwise False. If empty() returns True it doesn’t guarantee that a subsequent call to put() will not block. Similarly, if empty() returns False it doesn’t guarantee that a subsequent call to get() will not block.
Queue.full()
Returns True if the queue is full, False otherwise. If full() returns True it doesn’t guarantee that a subsequent call to get() will not block. Similarly, if full() returns False it doesn’t guarantee that a subsequent call to put() will not block.
Queue.put(item[, block[, timeout]])
Put item into the queue. If optional args block is true and timeout is None (the default), block if necessary until a free slot is available. If timeout is a positive number, it blocks at most timeout seconds and raises the Full exception if no free slot was available within that time. Otherwise (block is false), put an item on the queue if a free slot is immediately available, else raise the Full exception (timeout is ignored in that case).
Queue.get([block[, timeout]])
Remove and return an item from the queue. If optional args block is true and timeout is None (the default), block if necessary until an item is available. If timeout is a positive number, it blocks at most timeout seconds and raises the Empty exception if no item was available within that time. Otherwise (block is false), return an item if one is immediately available, else raise the Empty exception (timeout is ignored in that case).
Queue.task_done()
Indicates that a formerly enqueued task is complete. Used by queue consumer threads. For each get() used to fetch a task, a subsequent call to task_done() tells the queue that the processing on the task is complete.
If a join() is currently blocking, it will resume when all items have been processed (meaning that a task_done() call was received for every item that had been put() into the queue).
Raises a ValueError if called more times than there were items placed in the queue.
Queue.join()
Blocks until all items in the queue have been gotten and processed.
The count of unfinished tasks goes up whenever an item is added to the queue. The count goes down whenever a consumer thread calls task_done() to indicate that the item was retrieved and all work on it is complete. When the count of unfinished tasks drops to zero, join() unblocks.
Difference between Stack and Queue Data Structures
1: Which of the following data types is immutable in Python?
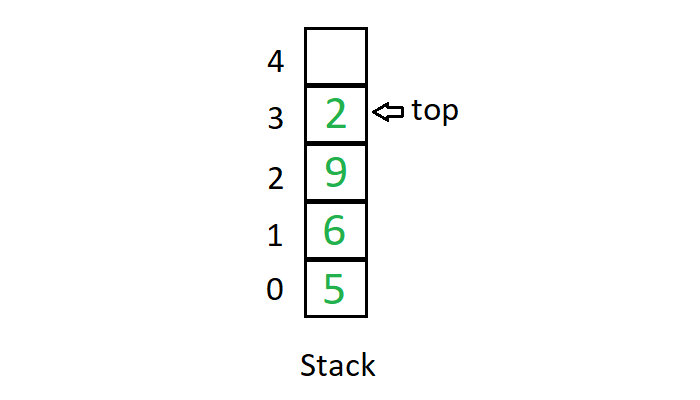
A stack is a linear data structure in which elements can be inserted and deleted only from one side of the list, called the top. A stack follows the LIFO (Last In First Out) principle, that is , the element inserted at the last is the first element to come out. The insertion of an element into stack is called push operation, and deletion of an element from the stack is called pop operation. In stack we always keep track of the last element present in the list with a pointer called top.
Learn to code from industry experts! Enroll here
The diagrammatic representation of stack is given below:
A queue is a linear data structure in which elements can be inserted only from one side of the list called rear, and the elements can be deleted only from the other side called the front. The queue data structure follows the FIFO (First In First Out) principle, that is, the element inserted at first in the list, is the first element to be removed from the list. The insertion of an element in a queue is called an enqueue operation and the deletion of an element is called a dequeue operation. In queue we always maintain two pointers, one pointing to the element which was inserted at the first and still present in the list with the front pointer and the second pointer pointing to the element inserted at the last with the rear pointer.
The diagrammatic representation of queue is given below:
Difference between Stack and Queue Data Structures
| Stacks | Queues |
|---|---|
| Stacks are based on the LIFO principle, i.e., the element inserted at the last, is the first element to come out of the list. | Queues are based on the FIFO principle, i.e., the element inserted at the first, is the first element to come out of the list. |
| Insertion and deletion in stacks takes place only from one end of the list called the top. | Insertion and deletion in queues takes place from the opposite ends of the list. The insertion takes place at the rear of the list and the deletion takes place from the front of the list. |
| Insert operation is called push operation. | Insert operation of queue is called enqueue operation. |
| Delete operation is called pop operation. | Delete operation of queue is called dequeue operation. |
| In stacks we maintain only one pointer to access the list, called the top, which always points to the last element present in the list. | In queues we maintain two pointers to access the list. The front pointer always points to the first element inserted in the list and is still present, and the rear pointer always points to the last inserted element. |
| Stack is used in solving problems works on recursion. | Queue is used in solving problems having sequential processing. |
Queue Operations in Data Structure
What is a Queue?
A queue is a logical group of elements in which updates or changes are introduced at one side (the “back”) and existing items are deleted at the opposite end (the “front”). When an item is introduced to the queue, it moves from the back to the front, ready to be eliminated next. The queue’s newly acquired item will have to wait until the collection’s finish. This way of ordering is also known as first-in-first-out (FIFO) (first-in, first-out).
Operating systems employ a variety of queues to manage things within a system. The next job is frequently planned using a queuing approach in order to run programs as quickly as feasible while servicing the largest number of people possible. Furthermore, while we type, keystrokes might occasionally outweigh the text on the screen. The reason is that the computer is now engaged with other duties. The strokes of keys are queued in a file and eventually shown on the screen in the right sequence.
Different operations in Queue Data Structure.
The various operations of queue in data structure that helps the user to modify and manipulate the data present in the queue are:
- Enqueue operation: The term “enqueue” refers to the act of adding a new element to a queue. Where does a new individual go and wait in a standard queue at a ticket counter to join the queue? The individual walks to the back of the room and takes a seat. A new element in a queue is similarly added at the end of the queue.
- Dequeue operation: Dequeue is the process of deleting an item from a queue. We must delete the queue member that was put first since the queue follows the FIFO principle. We will delete the front element and make the element behind it the new front element because the element added initially will naturally be at the head of the queue.
- Front Operation: This works similarly to the peek operation in stacks in that it returns the value of the first element without deleting it.
- isEmpty Operation: The isEmpty() function is used to check if the Queue is empty or not.
- isFull Operation: The isFull() function is used to check if the Queue is full or not.