Table of Contents
Everybody will go for answers but a rational human being will go for reasons. Verbal reasoning is one of the major types of questions asked in every competitive examination. Verbal reasoning using logical Ben diagram is the most asked number calculation in the competitive exams like Bank exams Kerala PSC and other major competitive exams. Venn diagram is one of the methods which is used to solve the verbal reasoning questions. Through this blog Entri discusses how to effectively apply a Logical Venn diagram in order to solve verbal reasoning questions for competitive examinations which is specially anticipated for the year 2020.
What is a Logical Venn Diagram?
A Venn diagram (also called primary diagram, set diagram or logic diagram) is a diagram that shows all possible logical relations between a finite collection of different sets. If a collection of sets is given, they may be interrelated in different ways. All possible relations can be depicted using a venn diagram in order to have a clear idea that can be useful for the entire statistical calculations. Set means a group or collection of similar kinds of things. A collection of similar things numbers words can be depicted as a set. For example, a set of 35 people usually take tea in the morning, we can make a set of 35 people a set with names of persons who take tea every morning. For another example, if 25 people would like to have coffee in the morning, we can make another set of 25 people who would like to have coffee in every morning.
How to Prepare for Verbal Reasoning for Competitive Examinations
Venn Diagram composition
The venn diagram can be classified into two. The data venn diagram and venn diagram represents the logical relation. The methodology used to analyse both the venn diagrams are the same. Both of the venn diagrams will have a circle and may or may not have a rectangle.
The Circle
The circle represents each set. A circle drawn in a plane represents each set in the logical relation. The circles may intercept, overlap or may be detached or may include another circle according to the logical relation. If the circle overlaps that means both the sets share some number of equal members. If a circle includes another circle, the included circle is a subset of the other circle. All the members in the included circle will be there in the parent set.
The Rectangle or the Plane
The rectangle or plane is not mandatory in every logical venn diagram. Some of the aspirants will draw some will not. The rectangle or the plane where the circles are drawn represents the universal set. The universal set means the all collection of the possible things. It includes all the members of the all the set in the logical venn diagram. This may seem to be unwanted in hearing but is very important in calculation.
Download Entri for a Detailed Class on Verbal Reasoning
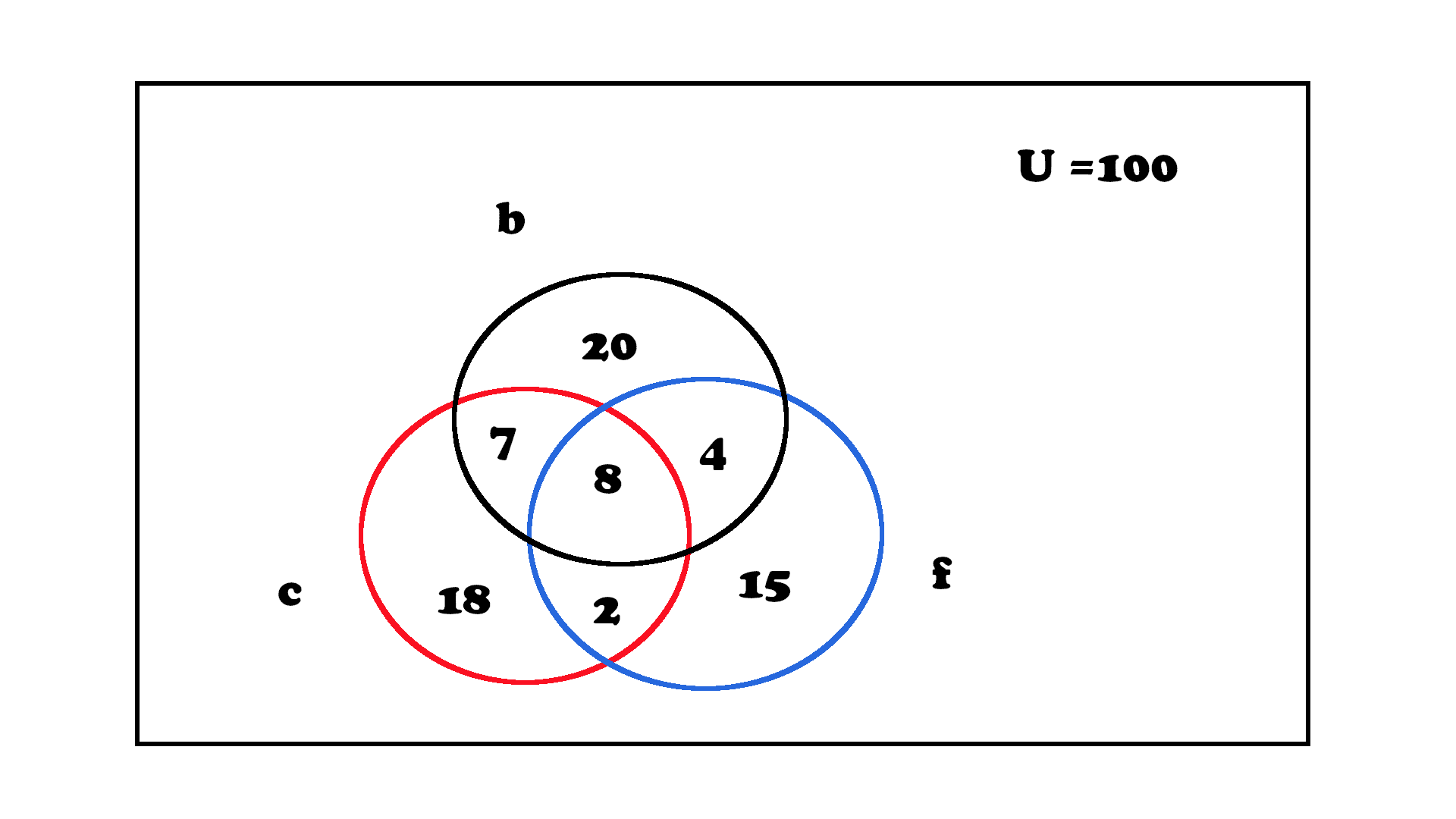
The Data Venn Diagram
The Red circle (c) = People who like to play cricket
The blue circle (f) = people who like to football
Black circle (b) = people who like to play badminton
Universal set (U) = total members the sports club
You can easily answer the following questions from the venn diagram.
How many wishes to play cricket but not any other game?
Ans: 18
How many people wish to play Badminton and football?
Ans: 4
How many people wish to play but not badminton?
Ans: 15 + 2 = 17
How many people wish to play not any games in the sports club?
Ans: Universal set number – All the sum of set (100 – (20+15+4+2+18+7+8) = 26)
The questions will go like this. It is easier to calculate all the answers if we know the logical Venn diagram. But no question providers will give you a logical Venn diagram in their questions. We have to figure out the logical venn diagram using the given facts. Always some facts accompanied by some questions is the usual way of asking verbal questions.
For the above questions the accompanying facts will be like this.
Out of the 100 people in a sports club 39 like badminton 29 like football and 35 like cricket. 8 people like all the three sports. 13 people like two sports at a time. There are 2 people who wish to play cricket and football and 7 people who wish to play cricket and badminton.
Click Here for More Sample Venn Daigram
How to Design a Data Venn Diagram
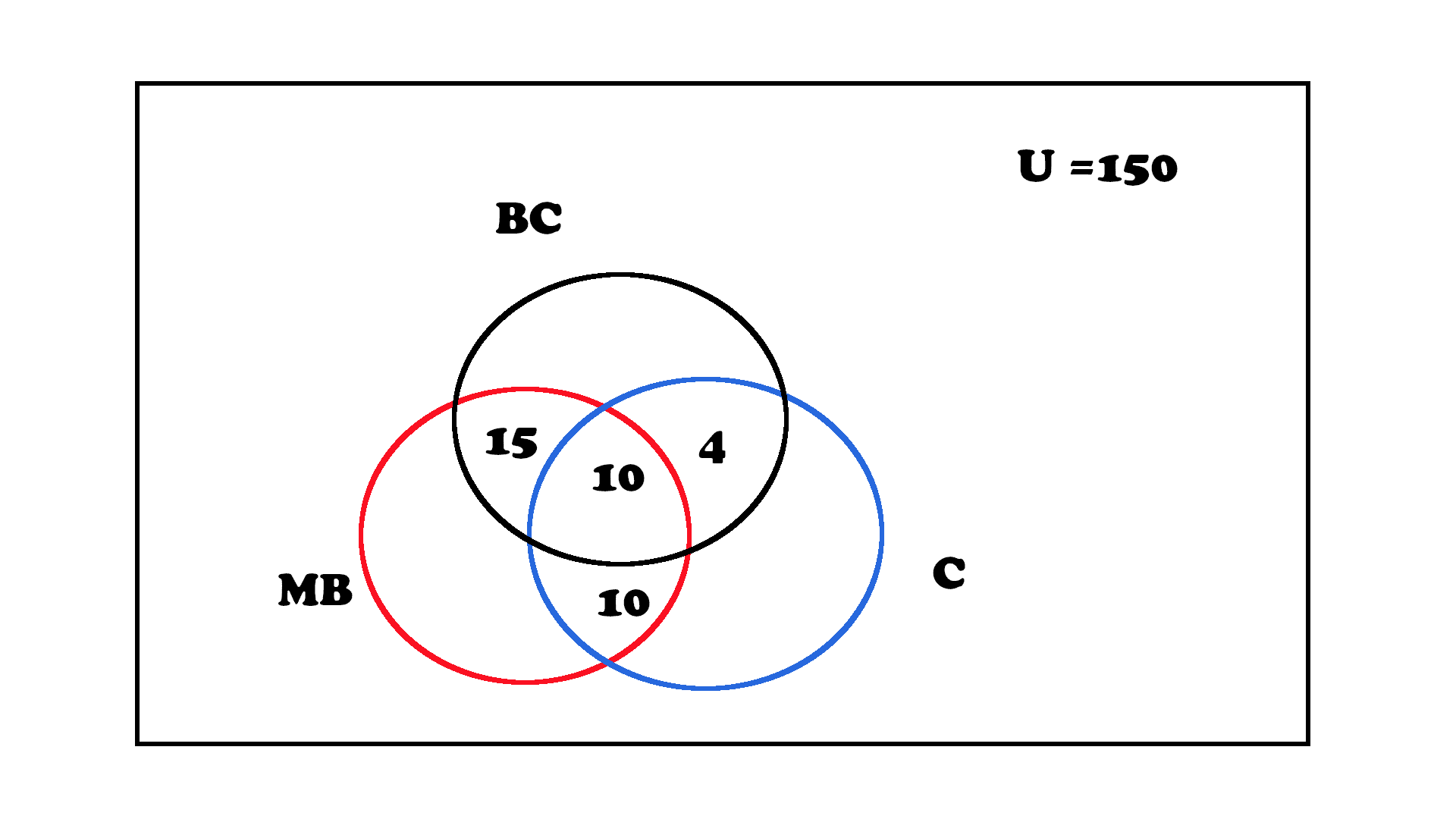
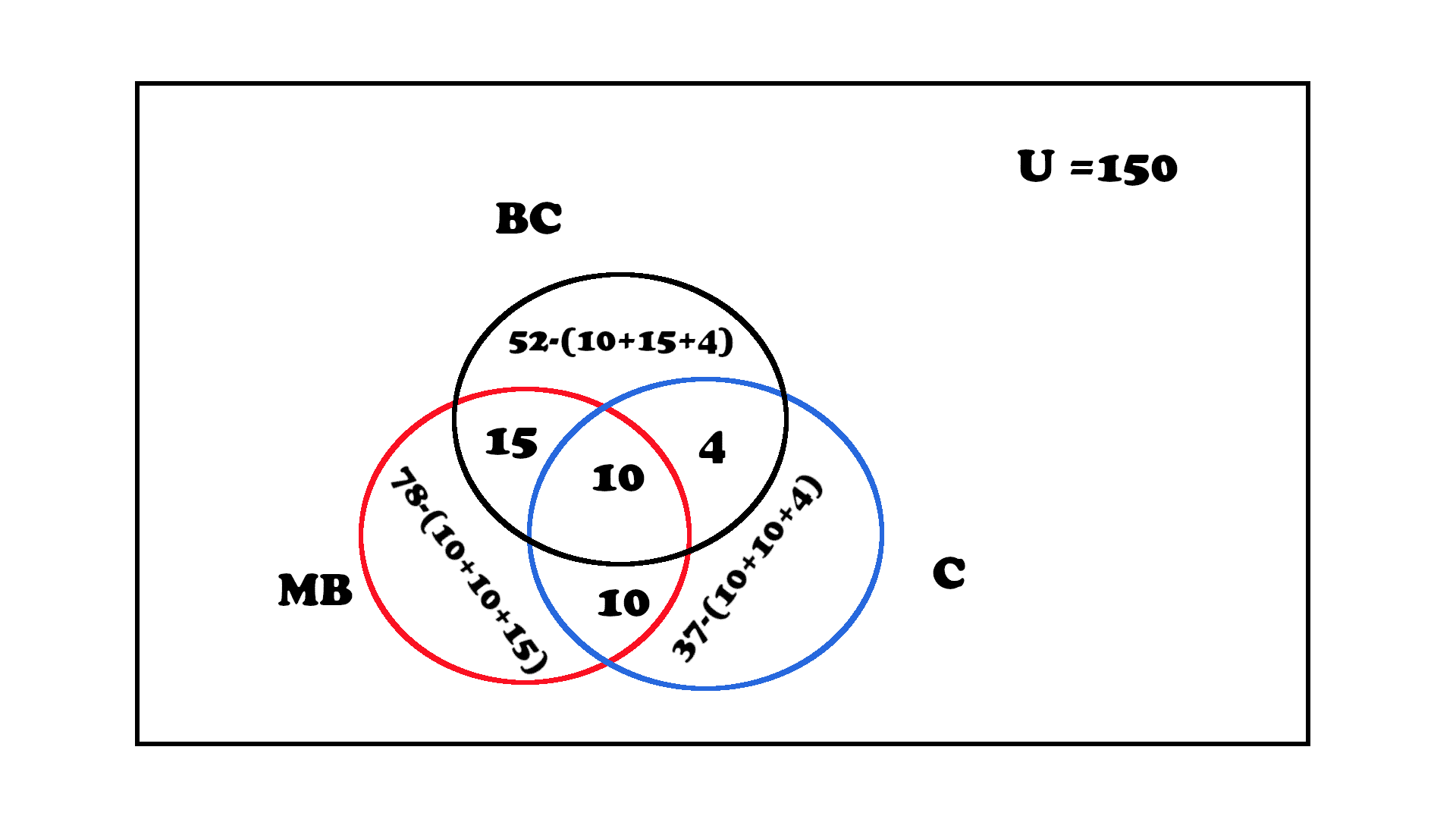
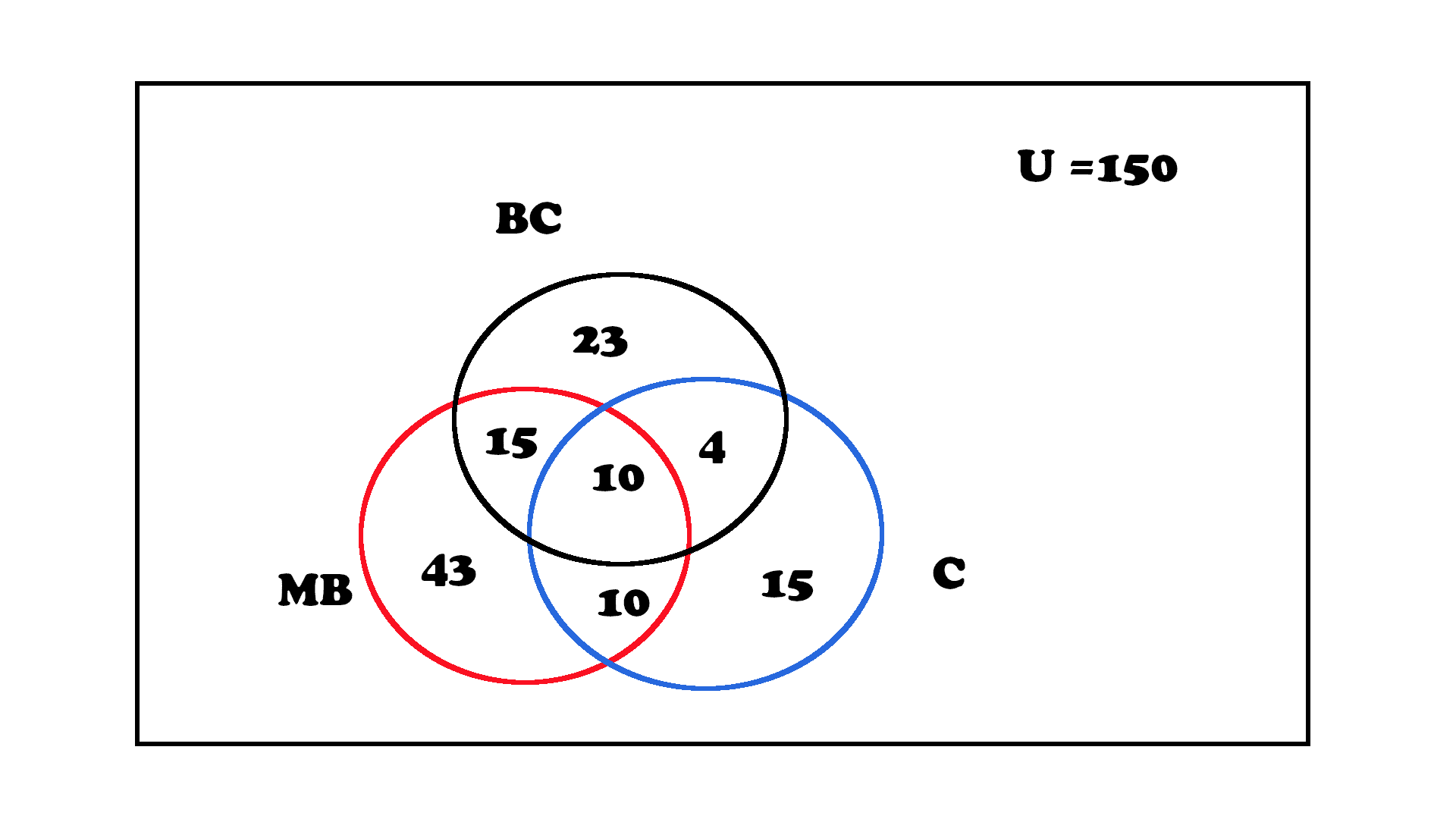
“In a housing colony of 150 people 39 people have a car 52 people have a bicycle and 78 people have a motorbike. There are 10 people who have everything. 10 people have car and a bike 4 people have car and a cycle and 15 people have cycle and a motorbike.”
The following methodology can be used to construct a logical when diagram for the above facts.
Step 1: Identify how many sets are there
Total 4. A car set, Bicycle set, Motorbike set and a universal set.
Step 2: Does all these set intersect each other
Yes
Step 3: Draw the circle diagram
Step 4: Mark first the number of people having all the vehicles, which means fill the vacuum of intersected space of all the three sets. (if it is directly given)
Step 5: Mark the number of people having two vehicles which means the intersected space of two sets. (if it is directly given)
Step 6: Finalising
The venn diagram representing Logical relations.
The venn diagram represents logical relations are always need to be solved by logical thinking. There is only one rule in that solving which is to understand the composition of the venn diagram.
- If a circle includes another circle the included circle is a subset of the other. The subset will have all the members of the superset or parent set or the other circle.
- If two circles are detached from each other then there will not be any relation with the two sets.
- If two circles intersect then the two sets will share some members.
For example, out of the given relations which of them represents beverages tea coffee milk tea powder and coffee powder.
Option (a)
Option (b)
Option (c)
Option (d)
The solution is Option (a) : Every tea is a beverage and every coffee is also a beverage. So, beverage circles should include Tea circle and Coffee circle. Every tea and coffee will have milk in common. So, tea circle and coffee circle should intersect each other. But no coffee will have tea powder and tea will have coffee powder. So, there should be circles of tea powder and coffee powder in a non-intersected space of the respective circle.
Click Here for More Model Questions on Verbal Reasoning
Conclusion
Entri makes every complexity simple. Make it simple and do it simple is the methodology adapted by entri in order to solve the complex problems. One can easily crack all kinds of logical venn diagrams for verbal reasoning for all minds of competitive examinations. Keep studying, keep winning.