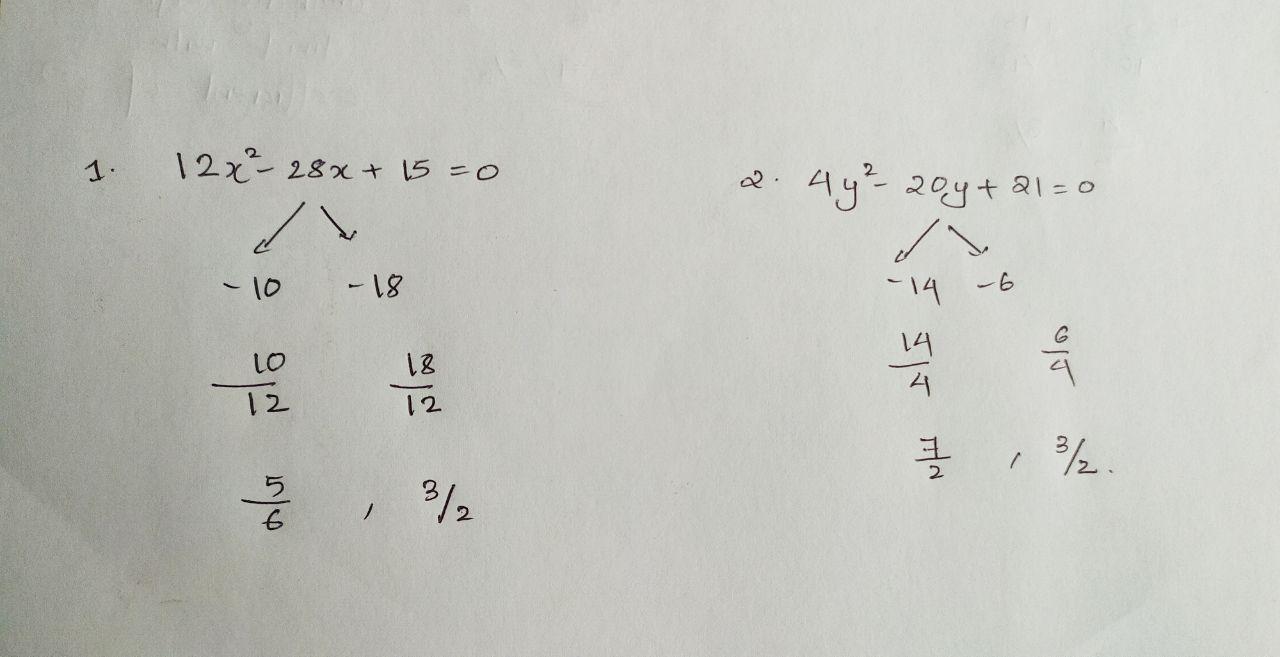The Quadratic Equation is an important topic in the Quantitative Aptitude section. Questions from this topic are asked in almost every competitive exam. Hence, let’s check out some Tips and Tricks to solve Quadratic Equation Bank Exams here. Before you start solving the Quadratic Equation questions, you must know the definition of it. What actually is the Quadratic Equation.
So, a Quadratic Equation is an equation that contains at least one squared term. It can be defined in the form of ax2 + bx + c = 0. Where a, b, and c are constants and ‘x’ is an unknown variable.
To clear the concept of the Quadratic Equation, you must be familiar with all the terminologies that are used.
Take free mock tests for upcoming bank exams in the Entri app
Quadratic Expression
A Quadratic Expression is something that can be simplified or factored. An expression cannot be solved for a variable but you can manipulate the terms that are given. Examples of a Quadratic Expression are:
x2 + 2x + 2
8x2 – 2x
4 – 5x – 10x2
6 – 12x2
Quadratic Function
A Quadratic Function can be represented in the form f(x) = ax2 + bx + c, where a, b & c are numbers with “a” not equal to zero. This function is given so that you can plot it on a graph. The graph of a quadratic equation is a Parabola.
Quadratic Equation Formulas & Basic Concepts
Now here are some basic concepts and important Quadratic Equation Formulas that are used to solve the questions. You should learn all the formulas by heart as without them you will not be able to solve the questions.
The Quadratic Equation Questions can be solved using these two methods:
- Standard Formula
- Factorization Method
Let’s understand these Quadratic Equation Concepts deeply.
Here we are explaining the traditional and shortcut methods to solve quadratic equation step by step
Check out this article on how to crack the banking exam with a good score here
1. Standard Formula
This formula is used to solve the Quadratic Equations easily and quickly. If an equation is in the form ax² + bx + c = 0, then the solution will be x = -b ± √(b² -4ac)/2a.
You will get two values due to the “+” and “-” sign. To understand this method better, we have given an example of it.
Question: Solve for x:- x2 + 4x – 8 = 0
Solution: Here in this equation, using the standard formula, the values of a, b and c are 1, 4, and -8 respectively.
So, the solution will be:
x = -b ± √(b² -4ac)/2a
x = -(-4) ± √(4)2 – 4(1)(-8)/ 2(1)
x = 4 ±√16 + 32/2
= 2 ± √48/2
x = 2 ± 2√12/2
x = 1 ± √12
Therefore, the two values of the equation are (1 + √12) and (1 – √12).
Ace Bank Exams ! Sign Up Now !!
2. Factorization Method
In the following questions, two equations (a) and (b) are given. You have to solve both the equations and find the relation between x and y.
Give answer (1) if x>y
(2) if x>=y
(3) if x<y
(4) if x<=y
(5) if x=y (or) the relation cannot be established.
Question 1
1. 40x2 – 47x + 12 =0
2. 5y2 – 51y + 54 =0
Normal method: (Factorization Method)
40x2 – 47x + 12 =0
40x2 – 32x-15x + 12 =0
8x(5x-4) – 3(5x-4) =0
(8x-3)(5x-4) =0
x= 3/8 or 4/5
5y2 – 51y + 54 =0
5y2 – 45y -6y + 54 =0
5y(y-9) -6(y-9) =0
(5y-6)(y-9) =0
y=6/5 or 9
Clearly x<y and the hence correct option is (3)
Now the shortcut method
Step 1: Similar to factorization split the middle term such that its product gives the last term and sum give the middle term.
For 40x2 – 47x + 12 =0, Sum = -47 and Product = 480. Hence the split terms are -32 and -15
Step 2: Now change the sign of split numbers, ie they become +32 and +15.
Step 3: Divide each of these numbers by the coefficient of x2
In this case, it becomes 32/40 and 15/40
Therefore x= 4/5, 3/8 ie the same as the result obtained using the traditional method. Repeat the same process for finding the values of y and compare them with x. We will obtain the same result as above.
Question 2
1. 12x2 – 28x + 15 =0
2. 4y2 – 20y + 21 =0
12x2 – 28x + 15 =0
12x2 -10x – 18x + 15 =0
2x(6x-5) -3(6x-5) =0
(2x-3)(6x-5)=0
x= 3/2, 5/6
4y2 – 20y + 21 =0
4y2 -14y – 6y + 21 =0
2y(2y-7) – 3(2y-7) =0
( 2y-3)( 2y-7) =0
y=3/2, 7/2
Here x<=y and the hence correct option is (4)
Now the shortcut method:
Let’s check out this method to find the solution based on the sign of coefficients in the equation
When we deal with the Quadratic Equations problem in Quantitative Aptitude, we should use time-saving tricks. The ideal & fast way to proceed, including the tricks, is given below:-
- Write down the table (given below) before exam starts, in your rough sheet, for use during the exam, Analyse the (+, -) signs in the problem, and refer to the table of signs. Follow the following steps to reach your answer in less than a minute.
STEP 1
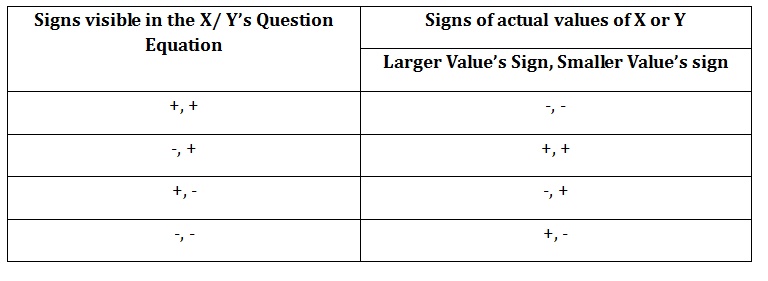
Firstly, when you enter the exam hall, you need to write down the following master table in your rough sheet instantly (only the signs):-
STEP 2:
Try solving the question instantly if possible, by checking whether + or – values can bring us to a conclusion.
For Example:
x2 + 7x + 12 = 0
y2 – 5y + 6 = 0
The signs of X’s equation are + and +, which means their solution is – and –. Both negative values.
The signs of Y’s equation are – and +, which means their solution values are + and +. Both positive values.
Obviously, X’s possible values are both negative… And Y’s possible values are both positive.
Obviously, the solution is X < Y.
So, any question with signs as “+, +” and “-, +” can be instantly solved, (unless it’s an unsolvable exception like x2 – 6x + 16 = 0, which can have no real integer as the answer. But this is a very rare occasion).
STEP 3:
If you visit Step 3, it means the question is not instantly solved in Step 2. Here, we write the 2 possible signs of each variable anyways, like plus or minus, in our rough sheet.
We must find the possible values of the variables. Remember, from the 2 symbols (+ or -) derived from the master table, the first symbol connects to the bigger value, and the second symbol connects to the smaller value, numerically.
Example :-
x2 – 12x + 32 = 0
y2 – 7y + 12 = 0
The question’s symbols are -, + which means both values will be positive for each variable, x and y.
x2 – 4x – 8x + 32 = 0
X (x – 4) – 4 (x – 8) = 0
X = 4, X = 8
y2 – 7y + 12 = 0
y2 – 4y – 3y + 12 = 0
y (y – 4) – 3 (y – 4) = 0
Y= 4, Y = 4
So, X >= Y
That’s it! To sum up, around 5 -6 questions are asked from this topic for most of the bank exams. Anyone can easily score full marks for this, all you need is practice. Follow us for future updates regarding all the exams. Enroll in Banking 2.0 – comprehensive study package for all upcoming bank exams of 2020-21.
| Related Courses | ||
| RRB Exams Coaching | RRB JE Online Coaching | SSC JE Online Coaching |
| SSC Online Coaching | UPSC Online Coaching | Bank Exam Coaching Online |